Vibrazione
Il termine vibrazione si riferisce in particolare a un'oscillazione meccanica attorno ad un punto d'equilibrio. L'oscillazione può essere periodica come il moto di un pendolo oppure casuale come il movimento di una gomma su una strada asfaltata; l'unità di misura della frequenza per le oscillazioni periodiche è l'hertz che corrisponde a quante volte, in un secondo, si ripresenta la stessa configurazione.

Le vibrazioni rappresentano un fenomeno desiderato in molti casi. Ad esempio nel funzionamento del diapason, e di molti strumenti musicali, o nei coni degli altoparlanti, necessari per il corretto funzionamento dei vari oggetti che li utilizzano. Più spesso, però, le vibrazioni non sono desiderate; possono disperdere energia e creare suoni e rumori indesiderati. Ad esempio, nel funzionamento delle automobili e dei motori in generale.
Gli studi sul suono e sulle varie vibrazioni sono strettamente collegati. I suoni, onde di pressione, sono generati da strutture vibranti (ad esempio le corde vocali) e le onde di pressione possono generare vibrazione di strutture. Quindi, quando si prova a ridurre un rumore, il problema è ridurre la vibrazione che lo provoca.
Tipi di vibrazioni[modifica | modifica wikitesto]
Vibrazioni libere: si verificano quando un sistema meccanico vibra e non è sottoposto ad alcuna forzante. Idealmente, se il sistema non fosse dotato di alcun tipo di attrito, smorzamento o comunque dispersione energetica, esso stesso continuerebbe a vibrare infinitamente nel tempo. Un sistema non sottoposto a forzante vibra poiché le sue condizioni iniziali erano (all'istante iniziale) non nulle. Un semplice esempio è il caso di una massa collegata ad un telaio per mezzo di una molla, molla che, all'istante iniziale, era ad esempio compressa.
Vibrazioni forzate: si hanno quando una forzante è applicata al sistema. Un esempio semplice è caratterizzato dalla lavatrice, il cui cestello, dotato di un ammortizzatore (per tale motivo definibile sistema vibrante), è continuamente sottoposto a forze rotanti, ossia alle forze d'inerzia generate dalla disposizione asimmetrica dei panni all'interno dello stesso.
Analisi delle vibrazioni[modifica | modifica wikitesto]
I fondamenti dell'analisi delle vibrazioni possono essere compresi studiando il modello semplice massa-molla-smorzatore interazione tra loro del tipo massa-molla-smorzatore (tale assunzione è comunque un'approssimazione in quanto nella realtà non esiste alcun comportamento perfettamente lineare ed è questo il caso ad esempio di presenza di giochi, di parametri fisici non costanti nel tempo, ecc.). Questo modello è un esempio di oscillatore armonico semplice e quindi la matematica usata per descrivere il relativo comportamento è identica ad altri oscillatori armonici semplici come il circuito RLC.
Nota: In questo articolo le graduali derivazioni matematiche non saranno incluse, ma verranno messi in luce le equazioni e i concetti principali nell'analisi delle vibrazioni. Per le derivazioni dettagliate occorre utilizzare i riferimenti all'estremità dell'articolo.
Vibrazioni libere non smorzate[modifica | modifica wikitesto]

Per iniziare l'analisi del sistema massa-molla-ammortizzatore si assuma che eventuali dispersioni siano trascurabili e che non ci siano forze esterne applicate alla massa (vibrazioni libere).
La forza applicata alla massa dalla molla è proporzionale all'allungamento "x"(si assume che la molla sia già compressa dal peso della massa). La costante di proporzionalità, k, rappresenta la rigidezza della molla ed ha unità di misura del tipo forza/distanza (ad esempio lbf/in or N/m)
La forza generata dalla massa è proporzionale all'accelerazione della massa come dato dalla seconda legge della dinamica di Newton.
La somma delle forze sulla massa allora genera questa equazione differenziale ordinaria:
Se si suppone di far iniziare a vibrare il sistema tirando la molla a una distanza “A” e si lascia andare, la soluzione alla suddetta equazione che descrive il movimento della massa è:
Questa soluzione dice che il sistema oscillerà con un movimento armonico semplice che ha ampiezza “A” e una frequenza di , ma che cosa è ? è una delle quantità più importanti nell'analisi delle vibrazioni ed è denominata frequenza naturale (o frequenza propria)
è definita per il sistema semplice massa-molla come:
Nota: La frequenza angolare () con unità di radianti/secondo è spesso usata nelle equazioni perché le semplifica, anche se normalmente viene convertita nelle unità “standard” per la frequenza (Hz o in modo equivalente cicli/secondo).
Conoscendo la massa e la rigidezza del sistema si può quindi determinare la frequenza a cui il sistema vibrerà dopo una perturbazione iniziale utilizzando la suddetta formula. Ogni sistema in vibrazione ha una o più frequenze naturali che si manifestano quando viene disturbato. Questa semplice relazione può essere usata per capire cosa accadrà a sistemi più complessi variando massa o rigidezza. Per esempio, la suddetta formula spiega perché quando un'automobile o un camion è completamente carico la sospensione sarà “più molle” di come si presenta a mezzo scarico perché la massa è aumentata e quindi ha ridotto la frequenza naturale del sistema.
Che cosa induce il sistema a vibrare senza l'azione di forze?[modifica | modifica wikitesto]
Queste formule descrivono il movimento risultante, ma non spiegano perché il sistema oscilla. Il motivo dell'oscillazione è dovuto alla conservazione dell'energia. Nel suddetto esempio la molla si è estesa da un valore “A” e quindi ha immagazzinato energia potenziale (). Una volta che si lascia andare la molla, questa prova a ritornare al proprio stato di riposo e nel processo accelera la massa. Nel punto in cui la molla ha raggiunto il punto di equilibrio non vi è più energia potenziale, ma la massa ha raggiunto la relativa velocità massima e quindi tutta l'energia potenziale è stata trasformata in energia cinetica (). La massa allora comincia a rallentare perché ora sta comprimendo la molla e nel processo che trasferisce l'energia cinetica nuovamente dentro il potenziale. Ciò che trasferisce avanti e indietro dell'energia cinetica nell'energia totale e potenziale nella molla induce la massa ad oscillare.
Nel nostro modello semplice la massa continuerà ad oscillare per sempre alla stessa grandezza, ma in un sistema reale c'è sempre qualcosa che dissipa l'energia e quindi il sistema tende a ritornare al proprio stato iniziale di riposo.
Vibrazioni libere smorzate[modifica | modifica wikitesto]

Ora si aggiunga un ammortizzatore viscoso al modello che produce una forza che è proporzionale alla velocità della massa. L'ammortizzazione è denominata viscosa perché modella gli effetti di un oggetto in un liquido. La costante di proporzionalità c, è denominata coefficiente di smorzamento ed ha unità di forza/velocità (lbf s/in | N s/m).
Sommando le forze sulla massa si ottiene la seguente equazione differenziale ordinaria:
La soluzione di questa equazione dipende dall'ammortizzazione. Se questa è abbastanza piccola il sistema tranquillo vibrerà, ma smetterà di vibrare col tempo. Questo caso è denominato underdamping (questo caso è di particolare interesse nell'analisi delle vibrazioni). Se si aumenta l'ammortizzazione appena al punto in cui il sistema non oscilla più si raggiungerà il punto di smorzamento critico (se l'ammortizzazione viene aumentata oltre lo smorzamento critico il sistema è denominato overdamped). Il valore che il coefficiente c deve raggiungere per lo smorzamento critico nel modello totale dell'ammortizzatore della molla è:
Per caratterizzare la quantità di ammortizzazione in un sistema si utilizza un rapporto denominato il coefficiente di smorzamento (anche conosciuto come rapporto di smorzamento e % di smorzamento critico). Questo coefficiente di smorzamento è giusto un rapporto dell'ammortizzazione reale sopra la quantità di ammortizzazione richiesta per raggiungere lo smorzamento critico. La formula per il coefficiente di smorzamento () del modello totale dell'ammortizzatore della molla è:
Per esempio, le strutture del metallo (per esempio la fusoliera dell'aeroplano, l'albero a gomito del motore) avranno fattori di circa 0.05 mentre le sospensioni automobilistiche di 0.2-0.3.
La soluzione al di sotto dello smorzamento critico per il modello totale dell'ammortizzatore della molla è la seguente:

Il valore della “X” della grandezza iniziale e del , spostamento di fase, è determinato dall'allungamento della molla. Le formule per questi valori possono essere trovate nei riferimenti.
I punti principali sono il termine esponenziale e la funzione coseno. Il termine esponenziale definisce quanto il sistema “si ammortizza rapidamente” - più grande è il coefficiente di smorzamento, più rapidamente si smorza a zero. La funzione coseno è la parte oscillante della soluzione, ma la frequenza delle oscillazioni è differente se ci si trova sotto il punto di smorzamento critico.
La frequenza in questo caso è denominata la frequenza naturale smorzata, il , ed è collegata con la frequenza naturale dalla seguente equazione:
La frequenza naturale smorzata minore della frequenza naturale “undamped”, ma per molti casi pratici il coefficiente di smorzamento è relativamente piccolo e quindi la differenza è trascurabile.
I diagrammi a lato con coefficienti di smorzamento di 0.1 e 0.3 mostrano come la vibrazione si smorza progressivamente col tempo. Ciò che si effettua in pratica è misurare sperimentalmente la vibrazione libera dopo una perturbazione (per esempio di un martello) ed allora determinare la frequenza naturale del sistema misurando il tasso di oscillazione ed il coefficiente di smorzamento misurando il tasso di deperimento. La frequenza naturale ed il coefficiente di smorzamento non sono importanti solo nella vibrazione libera, ma caratterizzano anche come un sistema si comporterà sotto la vibrazione forzata.
Vibrazione forzata con smorzamento[modifica | modifica wikitesto]
In questa sezione si analizza il comportamento del modello “massa-molla-smorzatore” quando si aggiunge una forza armonica. Una forza di questo tipo, per esempio, potrebbe essere generata da uno squilibrio di rotazione.
Se si sommano ancora le forze sulla massa si ottiene la seguente equazione differenziale ordinaria:
la soluzione di questo problema può essere scritta come:
Il risultato mostra come la massa oscillerà alla stessa frequenza, f, della forza applicata, ma con uno sfasamento pari a .
L'ampiezza della vibrazione “X” è definita dalla seguente formula.
Dove “r” è definito come il rapporto della frequenza armonica della forza armonica sopra la frequenza naturale “undamped” del modello “massa-molla-ammortizzatore”.
A questo proposito è interessante notare come l'ampiezza della risposta dell'oscillatore sia scomponibile in due contributi: il primo è dato da
ed è detto spostamento statico: è lo spostamento che il sistema subirebbe se la forza fosse costante (condizioni statiche) uguale a . Il secondo contributo viene detto fattore di amplificazione dinamico e rappresenta l'incremento subito dallo spostamento statico per effetto della variazione della forza nel tempo. Lo sfasamento, , è definito dalla seguente formula.
Il diagramma di queste funzioni, consistente nella risposta di frequenza del sistema, presenta una delle caratteristiche più importanti nella vibrazione forzata. In un sistema leggermente smorzato quando la frequenza di forzatura avvicina la frequenza naturale () l'ampiezza della vibrazione può risultare estremamente alta. Questo fenomeno è denominato risonanza.
Se la risonanza si presenta in un sistema meccanico può causare effetti dannosi conducendo al guasto finale del sistema. Di conseguenza uno dei motivi principali dell'analisi delle vibrazioni è di predire quando si può verificare la risonanza e determinare come operare per impedirne gli effetti. Il diagramma dell'ampiezza mostra che aggiungendo smorzamento si può ridurre significativamente la grandezza della vibrazione. Inoltre, la grandezza può essere ridotta se la frequenza naturale viene spostata dalla frequenza di forzatura cambiando la rigidezza o la massa del sistema. Se il sistema non può essere cambiato, può però essere variata la frequenza di forzatura (per esempio, cambiando la velocità della macchina che genera la forza).
I seguenti sono alcuni altri punti riguardanti le vibrazioni forzate indicate nei diagrammi di risposta di frequenza.
- Ad un dato rapporto di frequenza, l'ampiezza della vibrazione, X, è direttamente proporzionale all'ampiezza della forza (per esempio. Se la forza raddoppia, la vibrazione raddoppia a sua volta)
- Con la presenza di smorzamento minimo o nullo, la vibrazione ha luogo nella fase con la frequenza di forzatura quando il rapporto di frequenza r < 1 e 180° dalla fase se il rapporto r >1 di frequenza
- Quando r<<1 l'ampiezza è solo la deviazione della molla sotto la forza statica . Questa deviazione è denominata il . Quindi, quando r<<1 gli effetti dell'ammortizzatore e della massa sono minimi.
- Quando r>>1 l'ampiezza della vibrazione è realmente di meno della deviazione statica . In questa regione la forza generata dalla massa (F=ma) dominano perché l'accelerazione vista dalla massa aumenta con la frequenza. Fino a quando la deviazione vista nella molla, X, è ridotta in questa regione, la forza trasmessa entro la molla (F=kx) alla base è ridotta. Di conseguenza il sistema massa-molla-ammortizzatore sta isolando la forza armonica come isolamento antivibrante.
Che cosa causa la risonanza?[modifica | modifica wikitesto]
La risonanza è semplice da capire se si osserva la molla e la massa come elementi di stoccaggio di energia. La massa immagazzina energia cinetica e la molla immagazzina energia potenziale. Quando la massa e la molla non subiscono su di loro alcuna forza trasferiscono una quantità di energia proporzionale alla frequenza naturale. Applicare una forza alla massa ed alla molla è simile a spingere un bambino su un'altalena, dovete spingere al momento corretto se si desidera amplificare e aumentare l'oscillazione. Come nel caso dell'oscillazione, la forza applicata non deve essere necessariamente alta per ottenere grandi movimenti. Le spinte devono continuare a aggiungere l'energia al sistema.
L'ammortizzatore dissipa energia invece di immagazzinarla. Poiché la forza smorzante è proporzionale alla velocità, più è ampio il movimento più l'ammortizzatore dissipa l'energia. Di conseguenza un punto d'equilibrio si verificherà quando l'energia dissipata dall'ammortizzatore sarà uguale l'energia che è caricata dalla forza. A questo punto, il sistema ha raggiunto la relativa ampiezza massima e continuerà a vibrare a questa ampiezza finché la forza applicata rimane costante. Se non vi sono fonti di smorzamento, non si ha nulla nel sistema in grado di dissipare l'energia e quindi il moto continuerà teoricamente all'infinito.
Applicando forze “complesse” al modello Massa-Molla-Smorzatore[modifica | modifica wikitesto]
Nella sezione precedente è stata applicata al modello soltanto una forza armonica semplice, ma questa può estendersi considerevolmente per mezzo di due potenti strumenti matematici. Il primo è la trasformata di Fourier che prende un segnale in funzione del tempo (dominio del tempo) e lo divide nei relativi componenti armonici in funzione della frequenza (dominio della frequenza). Per esempio, applicando una forza al modello massa-molla-smorzatore che ripete il seguente ciclo: una forza uguale a 1 Newton per 0,5 secondi e poi nessuna forza per 0,5 secondi. Questo tipo di forza ha la frequenza di un 1 hertz (onda quadra).

La trasformata di Fourier dell'onda quadra genera uno spettro di frequenza che presenta l'intensità delle armoniche che compongono l'onda quadrata. La trasformata di Fourier può anche essere usata per analizzare funzioni non periodiche le funzioni per le quali le forze (per esempio impulsi) e le conseguenti funzioni sono casuali. Con l'avvento dei moderni calcolatori la trasformata di Fourier è utilizzata quasi sempre come Trasformata di Fourier veloce (FFT).
Nel caso della nostra onda quadrata, il primo componente è realmente una forza costante di 0,5 Newton ed è rappresentato da un valore di “0” hertz nello spettro di frequenza. Il componente seguente è un'onda seno di 1 hertz con un'ampiezza di 0,64. Ciò è indicata dalla linea a 1 hertz. I componenti restanti consistono in frequenze dispari e necessitano di una quantità infinita di onde seno per generare l'onda quadra perfetta. Quindi, la trasformata di Fourier permette di interpretare la forza come una somma delle forze sinusoidali che sono applicate al sistema anziché la forza più “complessa” (per esempio un'onda quadra).
Nella sezione precedente, la soluzione di vibrazione è stata data per una singola forza armonica, ma la trasformata di Fourier generalmente valuta le forze armoniche multiple. Il secondo strumento matematico, è il principio di sovrapposizione, che permette di sommare i contributi prodotti dalle singole forze se il sistema è lineare. Nel caso del modello molla-massa-ammortizzatore, il sistema è lineare se la forza della molla è proporzionale allo spostamento e lo smorzamento è proporzionale alla velocità nelle possibilità di movimento di interesse. Quindi, la soluzione al problema con un'onda quadra si ottiene sommando la vibrazione prevista da ogni forza armonica che si trova nello spettro di frequenza dell'onda quadra.
Modello di risposta di frequenza[modifica | modifica wikitesto]
Si può osservare la soluzione di un problema riguardante le vibrazione come un rapporto dell'ingreso/uscita dove la forza è l'input e l'uscita è la vibrazione. Se si rappresenta la forza e vibrazione nel dominio di frequenza (grandezza e fase) si può scrivere il seguente rapporto:
è denominato funzione di risposta di frequenza (è anche citata come funzione di trasferimento, anche se non è tecnicamente esatto) e ha sia una grandezza che il componente di fase (se rappresentato come un numero complesso, un componente reale ed immaginario). La grandezza della funzione di risposta di frequenza (FRF) è stata presentata in precedenza per il sistema della massa-molla-ammortizzatore.
La fase del FRF inoltre è stata presentata inizialmente come:
La figura inoltre mostra la rappresentazione di dominio di tempo della vibrazione risultante. Questa è calcolata effettuando una trasformata di Fourier inversa che converte i dati di dominio di frequenza in dominio di tempo. In pratica, questo calcolo è eseguito raramente perché lo spettro di frequenza fornisce tutte le informazioni necessarie

La funzione di risposta di frequenza (FRF) non deve essere calcolata necessariamente partendo dalla conoscenza dei valori della massa, dello smorzamento e della rigidezza del sistema, ma può essere misurata sperimentalmente. Per esempio, se applicate una forza conosciuta e ne valutate la frequenza, allora misurate la vibrazione risultante e potete calcolare la funzione di risposta di frequenza; in questo modo è possibile comunque caratterizzare il sistema. Questa tecnica è usata in campo sperimentale analisi modale per determinare le caratteristiche di vibrazione di una struttura.
Il battimento[modifica | modifica wikitesto]
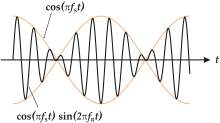
Il battimento è un fenomeno che avviene per somma di due vibrazioni di pari ampiezza, ma che differiscono l'un l'altra per una più o meno lieve differenza di frequenza, le quali periodicamente si sommano o si annullano, andando a formare un'unica forza che ha un andamento che potrebbe essere racchiuso tra due onde sinusali identiche e sfasate tra loro di 180°.
Vibrazioni sotto vari punti di vista[modifica | modifica wikitesto]
Vibrazioni strumentali (strumenti musicali)[modifica | modifica wikitesto]
La condizione fondamentale affinché si produca un suono è che sia messo in vibrazione un corpo vibrante e perché un corpo sia definito vibrante, è necessario che esso sia elastico. Una corda, ad esempio, viene definita vibrante quando viene sottoposta a tensione.
Per ottenere suoni acuti occorrono corde sottili, corte e ben tese; per ottenere suoni gravi occorrono corde spesse, lunghe e leggermente tese.
L'aria, come qualsiasi gas, può diventare un corpo vibrante purché sia contenuta in un tubo dalle pareti rigide che abbia almeno una via di comunicazione con l'esterno. I tubi che si utilizzano nella pratica musicale si distinguono in base alla loro imboccatura. Quest'ultima può essere:
- A Flauto: si ha quando la corrente d'aria immessa nel tubo s'incontra con uno spigolo tagliente.
- Ad ancia Semplice: si ha quando il suono è provocato dalle vibrazioni dell'ancia che si può adattare in una fenditura tagliata a becco, abbastanza larga da permettere un'intera oscillazione (Ancia semplice libera. Es. armonium) o in una fenditura più stretta che non la lascia passare la laminetta, consentendole di compiere soltanto mezza oscillazione (Ancia semplice battente. Es. clarinetto e sassofono).
- Ad ancia doppia: il cui suono è provocato dal chiudersi e dall'aprirsi di una stretta fessura formata da due sottilissime linguette di canna riunite ad un'estremità. Ad esempio, l'oboe e il fagotto.
I tubi possono essere anche aperti dai due lati (tubi aperti) o da un solo lato (tubi chiusi). Nel tubo aperto si forma un nodo al centro e due ventri ai lati, mentre nel tubo chiuso il ventre si forma alla fine e l'aria torna indietro. La conseguenza è che, a parità di lunghezza, un tubo chiuso produrrà un suono che è l'ottava bassa di un tubo aperto.
La frequenza, nei tubi, dipende:
- dall'ampiezza dell'apertura attraverso la quale si immette l'aria: più l'apertura è piccola, maggiore sarà il numero delle vibrazioni e più acuto sarà il suono;
- dalla rapidità con la quale l'aria è immessa nel tubo (dipende dall'esecutore);
- dalle dimensioni della colonna d'aria contenuta nel tubo: più è lungo il tubo, maggiore sarà la quantità d'aria in esso contenuta e più grave il suono prodotto.
Per quanto riguarda, invece, le piastre e le membrane, la vibrazione di questi strumenti è regolata dalla legge del fisico Chladni, il quale prese dei granelli di sabbia e li sparse sopra le piastre. Mettendoli in vibrazione, questi granelli si riunivano secondo alcune linee nodali (= linee di non vibrazione) e si accorse che si ottenevano questi disegni, più o meno geometrici.
Vibrazione di un motore[modifica | modifica wikitesto]
La vibrazione di un motore è data principalmente dalla sua struttura costruttiva, infatti a seconda del tipo di motore si potranno avvertire delle vibrazioni più o meno forti, per ridurre questo problema molte case costruttrici sono ricorse a vari sistemi per ridurre tali vibrazioni o per attutirle.
- I metodi per ridurre le vibrazioni consistono nell'equilibrare l'albero motore o di applicare l'equilibratore, un albero in sincronia con l'albero motore, che essendo munito di un peso decentrato dall'asse di rotazione, genera una vibrazione opposta a quella del motore, rinchiudendola o eliminandola definitivamente.
- I metodi per attutire le vibrazioni sono generalmente dati dall'applicazione di spessori di gomma, che assorbono gran parte della vibrazione.
Vibrazione da vibratore[modifica | modifica wikitesto]
Le vibrazioni del vibratore o delle macchine vibranti, vengono sfruttate generalmente dalle aziende o ditte, per migliorare un prodotto o una lavorazione, infatti se si pensa alle lavorazioni in campo edile, ed in particolare al cemento, questo viene sollecitato da vibrazioni per occupare tutti gli spazi vuoti, infatti senza tali vibrazioni il cemento si assesterebbe subito, senza occupare perfettamente tutto lo spazio a disposizione. Tali vibrazioni evitano quindi la formazione di zone “vuote” rendendo il cemento meno viscoso.
Effetti sulla salute[modifica | modifica wikitesto]

Nel terzo millennio si è sempre più dato importanza agli effetti delle vibrazioni fisiche sul corpo umano e su come prevenirne i danni, attualmente sono ancora in corso diversi studi sui diversi distretti del corpo, ma si è già arrivati a dimostrare come siano deleteri per la colonna vertebrale.[2]
In ambito ermetico si attribuisce capacità vibratoria anche ai pensieri, ritenuti in grado di creare delle strutture energetiche, o campi morfici, capaci di influire su quelle dimensioni della realtà con cui entrano in risonanza.[3] Il ristabilimento della salute consiste così nel reintegro di una vibrazione armonica tra le varie dimensioni, fisica, emotiva e mentale, che compongono la persona, servendosi di strumenti quali ad esempio la musica.[4]
Note[modifica | modifica wikitesto]
- ^ Da Acústica elemental, di J. Cabello e Roig, Madrid, Librería de la viuda de Hernando y C.ª, 1892.
- ^ ISPESL Vibrazioni meccaniche nei luoghi di lavoro: stato della normativa Archiviato il 5 luglio 2011 in Internet Archive.
- ^ Cfr. il terzo principio dell'ermetismo ne Il Kybalion, Venexia, Roma 2000: «Niente è immobile; tutto si muove; tutto vibra».
- ^ Alessio Di Benedetto, All'origine fu la vibrazione. Nuove e antiche conoscenze tra fisica, esoterismo e musica, a cura di T. Bosco, Nexus, 2008.
Bibliografia[modifica | modifica wikitesto]
- Rao, Singiresu, Mechanical Vibrations, Addison Wesley, 1990, ISBN 0-201-50156-2
- Thompson, W.T., Theory of Vibrations, Nelson Thornes Ltd, 1996, ISBN 0-412-78390-8
- Den Hartog, J. P., Mechanical Vibrations, Dover Publications, 1985, ISBN 0-486-64785-4
- Timoshenko, S. Vibration Problems In Engineering, Van Nostrand, 1937
- Thermotron Industries, Fundamentals of Electrodynamic Vibration Testing Handbook
- Nelson Publishing, Evaluation Engineering Magazine
- Cincinnati Sub-Zero, Inc., http://www.cszindustrial.com/Media/White-Papers.aspx
Voci correlate[modifica | modifica wikitesto]
- Attenuazione
- Moto armonico forzato senza smorzamento
- Risonanza (fisica)
- Rumore (acustica)
- Meccanica Quantistica
- Oscillatore armonico
- Suono
- Dinamica strutturale
- Mass damper
- Onda (fisica)
- Trasformata di Fourier
- Convenzione per la protezione dell'ambiente di lavoro (inquinamento dell'aria, rumori e vibrazioni), 1977
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «vibrazione»
Wikizionario contiene il lemma di dizionario «vibrazione» Wikimedia Commons contiene immagini o altri file su vibrazione
Wikimedia Commons contiene immagini o altri file su vibrazione
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) vibration, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Opere riguardanti Vibrazione, su Open Library, Internet Archive.
- Tesi di Laurea sulle vibrazioni del corpo umano in un veicolo, su meccanicaweb.it.
- Sito dedicato alla fisica delle onde, (università di Modena e Reggio Emilia), Fisica-onde-musica
| Controllo di autorità | J9U (EN, HE) 987007538793705171 |
|---|

































