Test Z
Il test Z (o, dall'inglese, Z-test) è un test statistico di tipo parametrico con lo scopo di verificare se il valore medio di una distribuzione si discosta significativamente da un certo valore di riferimento.
Il test Z bilaterale per la verifica d'ipotesi su un valore medio[modifica | modifica wikitesto]
Il test Z bilatero si utilizza nei casi in cui si intende verificare l'ipotesi che il valore medio di una popolazione non si discosti significativamente da un certo valore costante μ0.
Quando – nell'indagine campionaria – si vuole valutare l'ipotesi nulla:
contro l'ipotesi alternativa bidirezionale:
al livello di significatività α, si considera la statistica test:
dove
- è la v.c. media campionaria. Questa è distribuita normalmente se la popolazione è normale; se invece la popolazione non è normale, per il teorema centrale del limite si può comunque affermare che la media campionaria tenda alla normalità per n tendente a infinito, e quindi si può ben approssimare ad una distribuzione normale per valori di n elevati. Standardizzando rispetto a μ0 si ottiene la normale standard di media 0 e varianza 1.
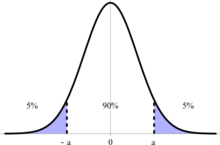
Per il test consideriamo una realizzazione campionaria della statistica ottenuta a partire dai dati campionari. Nota la dimensione campionaria n e la deviazione standard σ, la regione di rifiuto del test è costituita da quei valori della z empirica tali che:
Quindi se , siamo nella regione di rifiuto e vale H1.
Quindi, con una probabilità di errore α (errore di prima specie), la media di universo è diversa dal valore medio ipotizzato.
Varianza ignota[modifica | modifica wikitesto]
Se, come spesso accade nella realtà, non si conosce la varianza σ2 della popolazione, la si stima su base campionaria con lo stimatore varianza corretta del campione, ovvero la varianza campionaria:
- ,
la cui realizzazione campionaria è la stima della varianza di universo.
In questo caso il test non si chiama più test z, ma test t perché la distribuzione di probabilità della statistica test è una T di Student con n − 1 gradi di libertà. La verifica d'ipotesi è analoga al test z (si confronta la t empirica con il quantile di ordine α/2 delle T a n − 1 gradi di libertà).







