Potenza elettrica
In elettrotecnica si definisce potenza elettrica il flusso di lavoro elettrico per unità di tempo che, tramite la definizione di tensione e corrente, si esprime attraverso l'equazione[1]:
dove è la potenza elettrica erogata o assorbita da un componente elettrico soggetto a una tensione elettrica e una corrente , entrambe potenzialmente variabili nel tempo. Generalmente nel caso di tensioni e correnti variabili nel tempo si utilizza la potenza media.
Definizione[modifica | modifica wikitesto]
La forza esercitata da un campo elettrico su una carica elettrica elementare è , quindi il lavoro elettrico elementare svolto dalla forza lungo una traiettoria infinitesima è .[2] Definita la potenza elettrica come il flusso di lavoro elettrico nell'unità di tempo, allora si ha:[1]
Introducendo la definizione di tensione elettrica come il lavoro elettrico elementare compiuto per spostare una carica elementare in un campo elettrostatico lungo una traiettoria infinitesima [3] e definita l'intensità di corrente come la quantità di carica che fluisce attraverso una superficie nell'intervallo di tempo [4], allora, sostituendo le due definizioni nell'equazione della potenza elettrica, si ottiene:[1]
Corrente continua[modifica | modifica wikitesto]
In corrente continua i valori di tensione e corrente sono costanti nel tempo; è quindi possibile non considerare la dipendenza dal tempo e di conseguenza ottenere e . Tutta la potenza fornita dai generatori viene dissipata sui resistori del circuito per via dell'effetto Joule, quindi per la legge di Ohm si ha che dove è al resistenza o, dualmente, dove è la conduttanza. Secondo la convenzione degli utilizzatori allora si ha che la potenza assorbita dall'utilizzatore è:[5]
La potenza in corrente continua è misurata in watt (simbolo W) e, scelta la convenzione degli utilizzatori, la potenza è entrante nel bipolo mentre, dualmente, per la convenzione dei generatori la potenza va considerata uscente.
Corrente alternata[modifica | modifica wikitesto]

In corrente alternata i valori di tensione e corrente sono variabili nel tempo secondo un regime sinusoidale, si ha quindi che scelta una pulsazione (dove è la frequenza) le funzioni di tensione e corrente sono:
Indicato con lo sfasamento tra tensione e corrente, ovvero il ritardo di fase della corrente rispetto alla tensione che ha valore compreso tra e determinata la relazione tra i valori di picco i valori efficaci di tensione e corrente allora la potenza istantanea su un generico bipolo alimentato in corrente alternata è data da:
tramite l'uso delle formule di Werner si ricava:
La funzione della potenza è quindi una funzione periodica con pulsazione doppia (e quindi un periodo dimezzato) rispetto a quella della tensione e della corrente ed è riscrivibile come la somma di due componenti . Il primo termine è la potenza costante , rappresenta la potenza assorbita dal bipolo che viene trasformata in calore per effetto Joule o in lavoro utile nelle macchine elettriche, il secondo termine invece è la potenza fluttuante rappresenta la potenza alternativamente immagazzinata e ceduta dal bipolo.
Potenza attiva[modifica | modifica wikitesto]
La potenza attiva o potenza reale è definita come la media della potenza sul periodo , di conseguenza si ha:
Risolvendo l'integrale si determina che la potenza fluttuante ha valore medio nullo in un periodo quindi la potenza costante coincide con la potenza attiva:
Analogamente a quanto avviene per la potenza in corrente continua è misurata in watt e scelta la convenzione degli utilizzatori la potenza è entrante nel bipolo mentre dualmente per la convenzione dei generatori la potenza va considerata uscente. Il suo valore dipende dai valori efficaci di tensione e corrente e oltre che dal fattore di potenza . Scelto il fattore di potenza positivo, ovvero compreso tra , allora la potenza attiva assume valore massimo quando tensione e corrente sono in fase, ovvero per mentre raggiunge il suo valore minimo (nullo) quando sono in quadratura, ovvero per .
Considerato che il lavoro elettrico assorbito in un certo intervallo di tempo è allora risolvendo separatamente i due integrali si ha:
Se allora si può assumere quindi considerato che è possibile trascurare il termine della potenza fluttuante e ottenere che .
Potenza reattiva[modifica | modifica wikitesto]
Alcuni bipoli (bipoli reattivi o elementi d'accumulo) come induttori e condensatori sono in grado di immagazzinare energia e cederla successivamente. Poiché gli scambi avvengono in modo conservativo (sotto l'ipotesi di idealità dei componenti), l'energia complessivamente ceduta e assorbita in un periodo è nulla, come evidenziato dal termine in sen φ (potenza reattiva istantanea) nella formula della potenza istantanea. L'effetto complessivo è che la corrente e la tensione vengono sfasate, rendendo spesso necessario introdurre nel circuito un condensatore per il rifasamento del carico.
Per tenere conto di questo fenomeno, si introduce la potenza reattiva che in regime sinusoidale viene definita come la massima potenza reattiva istantanea, cioè:
Di nuovo è l'angolo di sfasamento. In regimi periodici non sinusoidali la definizione di potenza reattiva è meno intuitiva (vedere sotto). In regime sinusoidale è la parte immaginaria della potenza complessa. L'unità di misura è preferibilmente il voltampere reattivo (var).
Partendo da tensione v(t) e corrente i(t) istantanei è possibile calcolare la potenza reattiva istantanea utilizzando la seguente formula[6]:
Da cui:
ponendo:
Potenza apparente[modifica | modifica wikitesto]
Per quanto non dissipino energia, i bipoli reattivi fanno sì che in alcuni intervalli di tempo la corrente che circola sia maggiore di quella necessaria ai carichi resistivi (e quindi anche la potenza istantanea ceduta dal generatore). Per dimensionare opportunamente conduttori e generatori si introduce la potenza apparente:
dove e sono il valore efficace della tensione e della corrente.
In regime sinusoidale, corrisponde all'ampiezza dell'oscillazione della potenza istantanea attorno al suo valore medio. In regimi periodici non sinusoidali la definizione è sempre il prodotto dei valori efficaci di tensione e corrente. Si misura in voltampere (VA).
Potenza complessa[modifica | modifica wikitesto]

Per comodità, definiamo la potenza complessa come fasore:
Questa grandezza esprime in modo compatto tutte le altre introdotte finora. In termini fasoriali, per un'impedenza , dove R è la resistenza e X la reattanza, si ha:
dove è il fasore della tensione e è il coniugato del fasore della corrente.
I tre valori di , e sono legati tra loro dal fattore di potenza.
Potenze assorbite da un bipolo[modifica | modifica wikitesto]
Considerato un bipolo di impedenza legata a tensione e corrente tramite la relazione e definita la potenza complessa allora si ha da cui si ottengono:
- Potenza complessa:
- Potenza apparente:
- Potenza attiva:
- Potenza reattiva:
Rappresentazione vettoriale[modifica | modifica wikitesto]
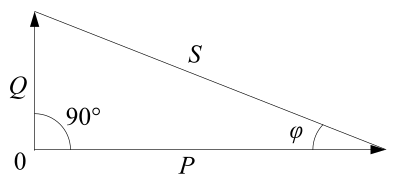
Immaginiamo di tracciare un diagramma polare di Argand-Gauss ove sugli assi X e Y siano rispettivamente rappresentate tensione e corrente. Si veda la tensione come un vettore giacente sull'asse X, che partendo dall'origine si dirige orizzontalmente verso destra. Se per la misura dello sfasamento si prende come riferimento la tensione, quest'ultima non ha componente immaginaria. La corrente si deve invece scomporre nella componente reale, che si sovrappone per direzione e verso alla tensione, e nella parte immaginaria, che appare ruotata di 90º (parte superiore del grafico) per le componenti induttive e −90º (parte inferiore del grafico) per le componenti capacitive. La potenza attiva è il prodotto fasoriale di tensione e parte reale della corrente, per cui giace sovrapposta all'asse della tensione (vettore P nel grafico). Il prodotto fasoriale tra tensione e parte immaginaria della corrente origina il fasore Q nel grafico, il cui verso dipende dalla natura dello sfasamento. Se in un circuito è presente sia una parte induttiva sia una capacitiva si può facilmente intuire come la potenza reattiva si compensi, in maniera totale o parziale, in quanto somma vettoriale dei due assi con uguale direzione ma verso opposto.
Dal grafico deriva che il legame tra le tre potenze può essere rappresentato anche graficamente tramite un triangolo rettangolo avente per ipotenusa il fasore della potenza apparente S e come cateti gli assi fasori della potenza attiva P e della potenza reattiva Q. Ovviamente l'angolo tra i cateti sarà un angolo di 90 gradi mentre l'angolo compreso tra P e S sarà l'angolo φ, cioè l'angolo di sfasamento tra tensione e corrente.
Teorema di Boucherot (o Metodo delle potenze)[modifica | modifica wikitesto]
La somma delle potenze attive (o reattive) erogate dai generatori in un circuito lineare e senza dissipazioni è uguale alla somma aritmetica delle potenze attive e alla somma algebrica delle potenze reattive (in quanto la potenza reattiva può essere tanto positiva quanto negativa: positiva se induttiva, negativa se capacitiva) assorbite dai bipoli.
Il teorema esprime il fatto che le due grandezze sono completamente indipendenti l'una dall'altra, giustificando, tra l'altro, l'uso di unità di misura diverse.
Il teorema dice quindi che quando sono presenti in cascata più carichi è possibile sommare tra loro le potenze attive e reattive ma non quelle apparenti, tranne nel caso in cui l'angolo di sfasamento (φ) sia uguale per tutti i carichi.
È notevole, per esempio, che alcuni generatori (come per esempio un motore asincrono fatto funzionare con scorrimento negativo) non siano in grado di fornire potenza reattiva. Se collegati in un generico circuito non sono infatti in grado di alimentare un carico (che normalmente ha anche una componente reattiva, anche solo per effetti di capacità parassita). Generatori di questo tipo non si comportano, elettricamente, come generatori di tensione nè come generatori di corrente, ma, più propriamente, come resistenze di valore negativo. Di conseguenza, sono solitamente schematizzati come resistenze negative per evidenziare questo fatto.
Partendo dal teorema di Tellegen, in forma fasoriale, si ha:
dove la somma è fatta sui bipoli del circuito (supponiamo di usare la convenzione degli utilizzatori). Poi, separiamo i termini dovuti a generatori e quelli dovuti a impedenze. Per i termini dovuti a generatori il prodotto rappresenta la potenza complessa erogata dal generatore (cambiata di segno, data la convenzione usata). Scriviamo i termini dovuti a impedenze sostituendo e otteniamo:
dove P e Q sono le potenze attive e reattive erogate dai generatori. Uguagliando a zero parte reale e parte immaginaria, otteniamo la tesi:
Sistemi polifase[modifica | modifica wikitesto]
Quanto descritto nella sezione precedente è riferito a un sistema monofase, costituito cioè da un circuito con un unico generatore.
Quando si passi a considerare un sistema costituito da più fasi, per esempio il sistema trifase comunemente utilizzato nella produzione, trasmissione e distribuzione elettrica, le potenze sono date dalle seguenti formule, valide per il sistema trifase ma generalizzabili a più fasi:
Se il sistema è simmetrico ed equilibrato, si possono esprimere anche in funzione delle grandezze di linea (come viene sempre fatto nei dati di targa) o delle grandezze di fase. Basta tenere conto della relazione tra grandezze di fase e di linea e si ottiene:
- .
Per ogni singola fase si ha ( è lo sfasamento tra tensione e corrente, ω è la frequenza di oscillazione, t è il tempo):
L'ultima equazione mostra che la potenza istantanea è composta da un primo termine costante che equivale alla potenza attiva e un secondo termine funzione sinusoidale del tempo. Sommando i valori ottenuti per le tre fasi, i secondi termini delle equazioni, essendo sfasati di 120º si annullano, e la potenza istantanea risulta uguale alla somma dei primi termini, costanti.
Corrente periodica non sinusoidale[modifica | modifica wikitesto]
Questi sistemi vengono studiati tramite l'analisi di Fourier, spesso scritta utilizzando i fasori (a partire dalla forma polare). Utilizzando questo strumento, si può calcolare la potenza attiva nella rete come somma delle potenze attive calcolate singolarmente per ciascuna armonica. In generale, quindi, bisognerà studiare separatamente il circuito per ciascuna delle armoniche (come si farebbe per il regime sinusoidale) disattivando i generatori (o le loro componenti) a frequenze diverse; solo alla fine si potranno sommare i risultati ottenuti per ciascuna armonica.
Un'ulteriore complicazione è data dal fatto che tensione e corrente possono avere forme d'onda diverse. Questo rende arduo definire la potenza reattiva in accordo al suo significato fisico; per analogia con la potenza attiva si definisce come somma delle potenze reattive calcolate per ciascuna armonica. Non vale più il teorema di Boucherot, e . Per tenere conto di questo effetto si definisce la potenza deformante, che è nulla per i circuiti che non modificano la forma d'onda. La potenza apparente viene invece definita utilizzando i valori efficaci (complessivi) di tensione e corrente; non è, quindi, la somma delle potenze apparenti.
Indicando con gli indici n i fasori della serie di Fourier e con lo sfasamento tra la tensione e la corrente , si definiscono:
Massimo trasferimento di potenza[modifica | modifica wikitesto]
Poiché, secondo il teorema di Thévenin, ogni bipolo resistivo (o adinamico) composto cioè da soli resistori, generatori indipendenti, generatori controllati o giratori può essere rappresentato come una serie tra un resistore (detto resistore equivalente di Thévenin, ) e un generatore di tensione indipendente (generatore equivalente di Thévenin, ), si può determinare la massima potenza erogabile dal bipolo. Ciò avverrà quando il bipolo stesso è chiuso su un resistore il cui valore di resistenza è uguale alla .
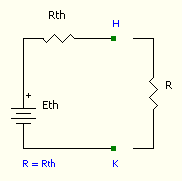
Applichiamo un generatore reale di tensione ai due morsetti una generica resistenza R. Sia quindi e . Sostituendo si ottiene la relazione tra la potenza erogata dal circuito e la resistenza applicata: . Per ottenere il valore massimo si deve annullare la derivata di questa funzione: . Sviluppando si ottiene , quindi ci interessa solo la derivata del denominatore: .
Ne consegue, tramite una semplice sostituzione, che la potenza massima erogata sarà data dal seguente valore: .
Il teorema si estende facilmente a circuiti lineari in regime periodico sinusoidale. In questo caso si vuole non solo che siano identiche le resistenze, ma anche che si annulli la reattanza (nella dimostrazione di cui sopra comparirà al denominatore sommata in quadratura alla resistenza). Questo risultato si ottiene, per esempio, ponendo un condensatore in parallelo a un carico induttivo in modo che vi sia risonanza. In questo modo i bipoli reattivi scambiano energia solo tra di loro, così che la potenza reattiva erogata dal generatore sia nulla e quindi la corrente erogata dal generatore sia solo quella che effettivamente compirà lavoro utile. Questo è di particolare importanza negli impianti elettrici, il cui adattamento prende il nome di rifasamento.
Note[modifica | modifica wikitesto]
- ^ a b c Arturi, 2017, p. 7.
- ^ Arturi, 2017, p. 1.
- ^ Arturi, 2017, p. 2.
- ^ Arturi, 2017, p. 4.
- ^ Turchetti, p. 225.
- ^ tenti, 2003.
Bibliografia[modifica | modifica wikitesto]
- Cesare Mario Arturi, Elettrotecnica 1: Reti elettriche e magnetiche, introduzione alla conversione magnetica, 2ª ed., Bologna, Società Editrice Esculapio, 2017 [2007], ISBN 978-88-7488-389-9. URL consultato il 10 settembre 2020.
- Enrico Turchetti, Romana Fasi, Elementi di Fisica, 1ª ed., Zanichelli, 1998, ISBN 88-08-09755-2.
- Tenti Paolo, A Time-Domain Approach to Power Term Definitions under Non-Sinusoidal Conditions.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su potenza elettrica
Wikimedia Commons contiene immagini o altri file su potenza elettrica
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) electric power, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN, FR) Potenza elettrica, su Enciclopedia canadese.
- Potenza elettrica in corrente alternata sinusoidale. Lezione
| Controllo di autorità | Thesaurus BNCF 38809 · LCCN (EN) sh85041875 · GND (DE) 4151723-4 · J9U (EN, HE) 987007535930605171 · NDL (EN, JA) 00561409 |
|---|










































![{\displaystyle \int _{0}^{t_{0}}P_{c}\ dt=\left[VI\cos \varphi \ t\right]_{0}^{t_{0}}=VI\cos \varphi \ t_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da371b1d55b92248e4d27ba1cc7bf8312edae7f4)
![{\displaystyle \int _{0}^{t_{0}}p_{f}\ dt=\left[-{1 \over 2\omega }\sin(2\omega t+\varphi )\right]_{0}^{t_{0}}=-{{\sin(\omega t_{0})\cos(\omega t_{0}+\varphi )} \over \omega }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186750845fd8073a48d0889b82a6aeb6555b2b98)
























































