Raggio di Einstein

Il raggio di Einstein è il raggio di un anello di Einstein, ed è importante nello studio delle lenti gravitazionali, poiché le distanze tipiche tra le immagini nelle lenti gravitazionali sono dell'ordine del raggio di Einstein.

Derivazione[modifica | modifica wikitesto]

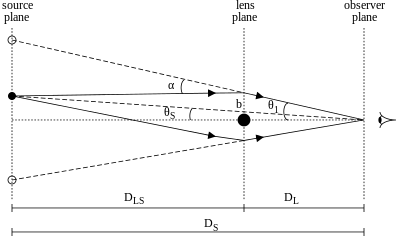
Nella derivazione seguente del raggio di Einstein si assume che tutta la massa M della galassia L che agisce da lente sia concentrata nel centro della galassia (massa puntuale).

Per una massa puntuale la deflessione può essere calcolata ed è uno dei classici test della teoria della relatività generale. Per angoli piccoli α₁ la deflessione totale dovuta ad una massa puntuale M è data (vedi metrica di Schwarzschild) da

\alpha _{1}={\frac {4G}{c^{2}}}{\frac {M}{b_{1}}}

dove

b₁ è il parametro di impatto (la distanza di massimo avvicinamento della traiettoria del fascio di luce al centro di massa)

G è la costante gravitazionale,

c è la velocità della luce.

Si nota che, per angoli piccoli e con l'angolo espresso in radianti, il punto b₁ di minima distanza dalla lente L, che forma un angolo θ₁ con la lente L a una distanza d_L è dato da b₁ = θ₁ d_L; possiamo quindi esprimere l'angolo di curvatura α₁ come

\alpha _{1}(\theta _{1})={\frac {4G}{c^{2}}}{\frac {M}{\theta _{1}}}{\frac {1}{d_{\rm {L}}}}

(eq. 1)

Se impostiamo θ_S come l'angolo sotto al quale l'osservatore vedrebbe la sorgente senza la lente (la quale di solito non è osservabile), e θ₁ come l'angolo osservato dell'immagine della sorgente rispetto alla lente, allora dalla geometria delle lenti si ricava (calcolando le distanze nel piano della sorgente) che la distanza verticale spazzata dall'angolo θ₁ ad una distanza d_S è la stessa della somma delle due distanze verticali θ_S d_S e α₁ d_LS. Questa è l'equazione della lente

\theta _{1}\;d_{\rm {S}}=\theta _{\rm {S}}\;d_{\rm {S}}+\alpha _{1}\;d_{\rm {LS}}

che può essere riscritta in funzione di θ₁

\alpha _{1}(\theta _{1})={\frac {d_{\rm {S}}}{d_{\rm {LS}}}}(\theta _{1}-\theta _{\rm {S}})

(eq. 2)

Imponendo l'uguaglianza delle due equazioni e facendo i calcoli, otteniamo

\theta _{1}-\theta _{\rm {S}}={\frac {4G}{c^{2}}}\;{\frac {M}{\theta _{1}}}\;{\frac {d_{\rm {LS}}}{d_{\rm {S}}d_{\rm {L}}}}

Per una sorgente situata dietro la lente, θ_S = 0, e l'equazione della lente per una massa puntuale assegna un valore caratteristico a θ₁ che viene chiamato raggio di Einstein, indicato con θ_E. Imponendo θ_S = 0 e risolvendo per θ₁ si ottiene

\theta _{E}=\left({\frac {4GM}{c^{2}}}\;{\frac {d_{\rm {LS}}}{d_{\rm {L}}d_{\rm {S}}}}\right)^{1/2}

Il raggio di Einstein per una massa puntuale fornisce una formula che rende adimensionali le variabili. In funzione del raggio di Einstein, l'equazione della lente per una massa puntuale diventa

\theta _{1}=\theta _{\rm {S}}+{\frac {\theta _{E}^{2}}{\theta _{1}}}

Sostituendo le costanti nell'equazione si ottiene

\theta _{E}=\left({\frac {M}{10^{11.09}M_{\bigodot }}}\right)^{1/2}\left({\frac {d_{\rm {L}}d_{\rm {S}}/d_{\rm {LS}}}{\rm {Gpc}}}\right)^{-1/2}{\rm {arcsec}}

In questa ultima forma, la massa è espressa in masse solari M_☉ e le distanze in Gigaparsec (Gpc).

Per un denso ammasso di galassie con massa M_c ≈ 10 × 10¹⁵ M_☉ alla distanza di 1 Gigaparsec (1 Gpc) questo raggio potrebbe essere lungo anche 100 arcosecondi (macrolente gravitazionale). Nel caso invece di una microlente gravitazionale (con una massa dell'ordine di M_☉) ad una distanza di circa 3 Kiloparsec (3 kpc), il raggio di Einstein risultante sarebbe dell'ordine del milliarcosecondo. Di conseguenza sarebbe impossibile osservare le immagini delle microlenti gravitazionali con le tecniche attuali.

Allo stesso modo, per il raggio di luce inferiore che raggiunge l'osservatore da sotto la lente, abbiamo

\theta _{2}\;d_{\rm {S}}=-\;\theta _{\rm {S}}\;d_{\rm {S}}+\alpha _{2}\;d_{\rm {LS}}

e

\theta _{2}+\theta _{\rm {S}}={\frac {4G}{c^{2}}}\;{\frac {M}{\theta _{2}}}\;{\frac {d_{\rm {LS}}}{d_{\rm {S}}d_{\rm {L}}}}

e perciò

\theta _{2}=-\;\theta _{\rm {S}}+{\frac {\theta _{E}^{2}}{\theta _{2}}}

L'argomento trattato può essere esteso al caso di lenti che hanno una distribuzione di masse qualunque, invece che una massa puntuale, esprimendo diversamente l'angolo di curvatura α. Le posizioni θ_I(θ_S) delle immagini possono così essere calcolate. Per piccole deflessioni questa mappatura è univoca e consiste in distorsioni delle posizioni osservate che sono invertibili. Questa è chiamata lente gravitazionale debole (weak lensing). Nel caso di grandi deflessioni si possono avere immagini multiple e una mappatura non invertibile: questa è una lente gravitazionale forte (strong lensing). Bisogna infine osservare che per ottenere un anello di Einstein la distribuzione di massa deve essere assialsimmetrica.