Programmazione dinamica
In informatica la programmazione dinamica è una tecnica di progettazione di algoritmi basata sulla divisione del problema in sottoproblemi e sull'utilizzo di sottostrutture ottimali.
Storia[modifica | modifica wikitesto]
Il termine è stato inizialmente utilizzato negli anni quaranta dal matematico Richard Bellman per descrivere il processo di soluzione dei problemi in cui sia necessario trovare le soluzioni migliori una dopo l'altra. Nel 1953 affinò il termine che assunse il significato moderno. Questo metodo fu studiato per l'analisi di sistemi e scopi ingegneristici riconosciuti dall'IEEE.
La parola programmazione in "programmazione dinamica" non ha alcuna particolare attinenza con la programmazione informatica. Originariamente il termine programmazione dinamica si applicava unicamente alla soluzione di alcuni tipi di problemi operativi al di fuori dell'area informatica, esattamente come nel caso della programmazione lineare. Un programma è semplicemente la pianificazione per l'azione che sarà prodotta. Per esempio una lista mirata di eventi, nel caso di una esibizione, è talvolta chiamata programma. Programmare, in questo caso, significa trovare un piano d'azione accettabile.
In generale[modifica | modifica wikitesto]
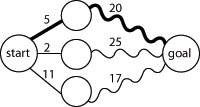
Sottostruttura ottimale significa che la soluzione ottimale al sottoproblema può essere utilizzata per trovare la soluzione ottimale dell'intero problema. Per esempio il cammino minimo da un vertice di partenza a un vertice di arrivo in un grafo aciclico può essere trovato calcolando dapprima il cammino minimo al punto di arrivo da tutti i vertici adiacenti, e quindi utilizzarlo per trovare il miglior cammino completo, come mostrato in Figura 1. In generale è possibile risolvere un problema con una sottostruttura ottimale utilizzando un processo a tre passi:
- suddividere il problema in sottoproblemi più piccoli;
- risolvere questi problemi in modo ottimale, utilizzando in modo ricorsivo questo processo a tre passi;
- usare queste soluzioni ottimali per costruire una soluzione ottimale al problema originale.
A loro volta i sottoproblemi sono risolti suddividendoli in sotto-sottoproblemi e così via, finché non si raggiungono alcuni casi facili da risolvere.

Dire che un problema ha sottoproblemi sovrapponibili equivale a dire che gli stessi sottoproblemi sono utilizzabili per risolvere diversi problemi più ampi. Per esempio nella successione di Fibonacci, F3 = F1 + F2 e F4 = F2 + F3, per il calcolo di entrambi i numeri è necessario il calcolo di F2. Siccome sia F3 sia F4 sono necessari per il calcolo di F5, un approccio ingenuo al calcolo di F5 può condurre a calcolare F2 due o più volte. Ciò si applica ogniqualvolta si presentino problemi sovrapponibili: un approccio ingenuo potrebbe sprecare del tempo ricalcolando la soluzione ottimale a sottoproblemi già risolti.
Al contrario, per evitare che ciò accada, occorre salvare la soluzione dei problemi già risolti. Quindi, se in seguito si necessita di risolvere lo stesso problema, è possibile riprendere e riutilizzare la soluzione già calcolata. Questo approccio è chiamato memoizzazione (non memorizzazione, anche se questo termine può risultare adeguato). Essendo sicuri che una particolare soluzione non sarà riutilizzata, è possibile liberarsene per risparmiare spazio. In alcuni casi è possibile calcolare in anticipo delle soluzioni a sottoproblemi, sapendo che successivamente saranno necessarie.
In sostanza la programmazione dinamica fa uso di:
La programmazione dinamica generalmente si basa su uno dei due seguenti approcci.
- Top-down: deriva direttamente dalla formulazione ricorsiva. Il problema è spezzato in sottoproblemi, questi sono risolti, e la soluzione è ricordata, nel caso sia necessario risolverli ancora. Si tratta di una combinazione di ricorsione e memoizzazione.
- Bottom-up: sono risolti innanzitutto tutti i sottoproblemi che possono essere necessari e successivamente sono utilizzati per costruire la soluzione a problemi più ampi. Questo approccio è leggermente migliore come dimensione degli stack e numero di chiamate alle funzioni, ma talvolta risulta non intuitivo prefigurarsi tutti i sottoproblemi necessari alla soluzione di un dato problema.
Alcuni linguaggi di programmazione possono memoizzare automaticamente con speciali estensioni [1] Archiviato il 2 settembre 2006 in Internet Archive. il risultato di una chiamata di funzione con un particolare insieme di argomenti, al fine di velocizzare la valutazione (meccanismo noto come call-by-need). Ciò è possibile solo per funzioni che non presentano effetti collaterali, cosa sempre vera in Haskell, ma raramente in linguaggi imperativi.
Esempi[modifica | modifica wikitesto]
Successione di Fibonacci[modifica | modifica wikitesto]
Una implementazione naïve di una funzione che cerchi l'n-mo membro della successione di Fibonacci, basato direttamente sulla definizione matematica:
function fib(n)
if n = 0 or n = 1
return n
else
return fib(n − 1) + fib(n − 2)
Notare che se si chiama fib(5), si produce un albero di chiamate che chiama più volte la medesima funzione sullo stesso valore:
fib(5)fib(4) + fib(3)(fib(3) + fib(2)) + (fib(2) + fib(1))((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
In particolare, fib(2) è stato calcolato interamente per due volte. In esempi più estesi sono ricalcolati molti più valori di fib, o sottoproblemi, portando ad un algoritmo a tempi esponenziali.
Ora, si supponga di avere un semplice oggetto mappa, m, che mappi ogni valore fib calcolato al proprio risultato, e si modifichi la funzione al fine di utilizzarlo ed aggiornarlo. La funzione risultante richiede solo un tempo O(n) invece che un tempo esponenziale:
var m := map(0 → 1, 1 → 1)
function fib(n)
if map m does not contain key n
m[n] := fib(n − 1) + fib(n − 2)
return m[n]
Questa tecnica di salvataggio dei valori già calcolati è chiamata memoizzazione. Si tratta dell'approccio top-down, visto che in primo luogo il problema è stato diviso in sottoproblemi, poi sono stati calcolati e salvati i valori.
Nel caso dell'approccio bottom-up, prima si calcola il più piccolo valore di fib, poi si costruiscono i valori più grandi a partire da questo. Anche questo metodo richiede un tempo O(n), visto che contiene un ciclo che si ripete n − 1 volte:
function fib(n)
var previousFib := 0, currentFib := 1
repeat n − 1 times
var newFib := previousFib + currentFib
previousFib := currentFib
currentFib := newFib
return currentFib
In entrambi questi esempi si è calcolato fib(2) solo una volta e poi lo si è utilizzato per calcolare sia fib(4) che fib(3), invece di calcolarlo ogni volta che questi ultimi valori vengono calcolati.
Scacchiera[modifica | modifica wikitesto]
Si consideri una scacchiera di n × n caselle e una funzione costo c(i, j) che restituisce un costo associato alla casella i,j (con i la riga e j la colonna). Per esempio (su una scacchiera 5 × 5),
+---+---+---+---+---+
5 | 6 | 7 | 4 | 7 | 8 |
+---|---|---|---|---+
4 | 7 | 6 | 1 | 1 | 4 |
+---|---|---|---|---+
3 | 3 | 5 | 7 | 8 | 2 |
+---|---|---|---|---+
2 | 2 | 6 | 7 | 0 | 2 |
+---|---|---|---|---+
1 | 7 | 3 | 5 | 6 | 1 |
+---+---+---+---+---+
1 2 3 4 5
tale che c(1, 3) = 5
Si abbia una pedina che possa partire in ogni casella del primo livello e che si voglia conoscere il cammino minimo (somma dei costi delle caselle visitate) per arrivare all'ultimo livello, assumendo che la pedina si possa muovere solo in avanti o in diagonale a sinistra-avanti o destra-avanti. Cioè una pedina in (1,3) può spostarsi su (2,2) (2,3) (2,4)
+---+---+---+---+---+
5 | | | | | |
+---|---|---|---|---+
4 | | | | | |
+---|---|---|---|---+
3 | | | | | |
+---|---|---|---|---+
2 | | x | x | x | |
+---|---|---|---|---+
1 | | | O | | |
+---+---+---+---+---+
1 2 3 4 5
Questo problema presenta una sottostruttura ottimale: la soluzione dell'intero problema risiede nelle soluzioni dei sottoproblemi. Si definisca la funzione q(i, j) come
- q(i, j) = minimo costo per raggiungere la casella (i, j)
Se è possibile trovare i valori di questa funzione per tutte le caselle al livello n, si prende il minimo e si segue il percorso inverso per arrivare al cammino minimo.
Data una qualsiasi casella è facile vedere che q(i, j) è uguale al minimo costo per arrivare a qualsiasi delle tre caselle al di sotto, visto che queste sono le uniche da cui può essere raggiunta, più c(i, j). Per esempio:
+---+---+---+---+---+
5 | | | | | |
+---|---|---|---|---+
4 | | | A | | |
+---|---|---|---|---+
3 | | B | C | D | |
+---|---|---|---|---+
2 | | | | | |
+---|---|---|---|---+
1 | | | | | |
+---+---+---+---+---+
1 2 3 4 5
Ora si definisca q(i, j) in termini leggermente più generali:
Questa equazione è abbastanza diretta. La prima linea è là semplicemente per rendere più semplice la ricorsività quando si ha a che fare con gli angoli, per cui si ha bisogno di una sola ricorsione. La seconda linea dice cosa succede al primo livello, per cui si ha qualcosa da cui partire. La terza linea, la ricorsione, è la parte importante. È sostanzialmente la stessa cosa che nell'esempio A,B,C,D. Da questa definizione è possibile creare un codice diretto e ricorsivo per q(i, j). Negli pseudocodici seguenti, n è la dimensione della scacchiera, c(i, j) è la funzione costo, e min() restituisce il minore tra un certo numero di valori:
function minCost(i, j)
if j < 1 OR j > n
return infinity
else if i = 1
return c(i, j)
else
return min( minCost(i-1, j-1), minCost(i-1, j), minCost(i-1, j+1) ) + c(i, j)
Questa funzione calcola solo il costo del cammino, non il cammino stesso. Si arriverà presto al cammino; in questo algoritmo, come nell'esempio dei numeri di Fibonacci, il calcolo del cammino è molto lento, poiché si spreca tempo nel ricalcolare più volte il medesimo cammino minimo. È comunque possibile calcolare il cammino più velocemente nella modalità bottom-up, ad esempio usando un array bidimensionale q[i, j] invece della precedente funzione. Questo perché quando si usa una funzione si ricomputa lo stesso cammino ed è possibile scegliere in precedenza quale valore calcolare.
C'è anche bisogno di sapere qual è il reale cammino. Il problema del cammino può essere risolto utilizzando un altro array p[i, j], un array predecessore. Questo array in sostanza dice qual è il cammino di provenienza. Si consideri il seguente codice:
function computeShortestPathArrays()
for x from 1 to n
q[1, x] := c(1, x)
for y from 1 to n
q[y, 0] := infinity
q[y, n + 1] := infinity
for y from 2 to n
for x from 1 to n
m := min(q[y-1, x-1], q[y-1, x], q[y-1, x+1])
q[y, x] := m + c(y, x)
if m = q[y-1, x-1]
p[y, x] := -1
else if m = q[y-1, x]
p[y, x] := 0
else
p[y, x] := 1
Ora il problema è semplicemente quello di individuare il minimo e stamparlo.
function computeShortestPath()
computeShortestPathArrays()
minIndex := 1
min := q[n, 1]
for i from 2 to n
if q[n, i] < min
minIndex := i
min := q[n, i]
printPath(n, minIndex)
function printPath(y, x)
print(x)
print("<-")
if y = 2
print(x + p[y, x])
else
printPath(y-1, x + p[y, x])
| Controllo di autorità | Thesaurus BNCF 22135 · LCCN (EN) sh85040313 · GND (DE) 4125677-3 · BNE (ES) XX543843 (data) · BNF (FR) cb11978098s (data) · J9U (EN, HE) 987007567971605171 · NDL (EN, JA) 00571739 |
|---|

