Numero armonico

Un grafico della crescita dell'n-esimo numero armonico $H_{n,1}$ con $n=\lfloor {x}\rfloor$ (linea rossa) insieme al suo limite asintotico $\gamma +\ln[x]$ (linea blu).

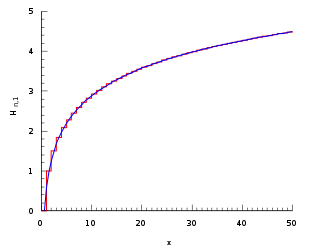
In matematica, per ogni intero naturale n si definisce come n-esimo numero armonico la somma:

$H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}$

Si tratta evidentemente di numeri razionali e si dimostra che le corrispondenti frazioni ridotte ai minimi termini hanno numeratore dispari e denominatore pari.

In concreto i primi termini della successione dei numeri armonici sono:

1, 3/2, 11/6, 25/12, 137/60, 49/20, 363/140, 761/280, 7129/2520, 7381/2520, 83711/27720, ...

I numeratori dei numeri armonici sono detti numeri di Wostenholme e costituiscono la successione A001008 dell'OEIS. I denominatori costituiscono la successione A002805 dell'OEIS.

I numeri armonici costituiscono le somme parziali della serie armonica, notoriamente divergente.

Numeri armonici alternati

I numeri armonici sono strettamente collegati a quelli che si possono chiamare numeri armonici alternati

$H'_{n}:=\sum _{k=1}^{n}(-1)^{k+1}{\frac {1}{k}}$ .

Questi sono le somme troncate della serie armonica alternata notoriamente convergente e sono esprimibili mediante i numeri armonici dalle formule

$H'_{2n}=H_{2n}-H_{n}\qquad H'_{2n+1}=H_{2n}-H_{n}+{\frac {1}{2n+1}}$

Espressione analitica

I numeri armonici (e quindi anche i numeri armonici alternati) si possono esprimere analiticamente come

$\,H_{n}=\gamma +\Psi (n+1)$

mediante la costante di Eulero - Mascheroni e la funzione digamma (e di conseguenza mediante la funzione gamma)

$\Psi (z)\equiv \psi _{0}(z):={\frac {d}{dz}}\ln \Gamma (z)={\frac {\Gamma '(z)}{\Gamma (z)}}.$

Numeri armonici generalizzati

Il concetto di numero armonico può essere generalizzato con la seguente definizione.

Fissati due interi naturali m ed n, si definisce come n-esimo numero armonico generalizzato di esponente m la somma:

$H_{n}^{(m)}:=\sum _{k=1}^{n}{\frac {1}{k^{m}}}$

Si può notare che i numeri armonici sono il caso particolare di numeri armonici generalizzati di esponente 1.

Per m negativi, si ottiene la somma di potenze di interi successivi

$\sum _{k=1}^{n}k^{|m|}$

che è strettamente legata ai polinomi di Bernoulli.

Collegamenti

I numeri armonici e i numeri armonici generalizzati che li comprendono si incontrano in numerose aree della matematica riferibili alla combinatoria e allo studio delle funzioni speciali. Essi intervengono nello studio di funzioni speciali particolari, ad es. della funzione poligamma della funzione polilogaritmo e della funzione zeta di Riemann; essi inoltre si incontrano in recenti sviluppi di elevata generalità, come le questioni collegate all'approssimazione di Hermite-Padé.

Bibliografia

• R. L. Graham, D. E. Knuth and O. Patashnik (1990): Concrete Mathematics, Addison-Wesley, p. 259.
• D. E. Knuth: The Art of Computer Programming. Addison-Wesley, Vol. 1, p. 615.

Voci correlate

• Identità con numeri armonici

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su numero armonico

Collegamenti esterni

• (EN) harmonic number, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Numero armonico, su MathWorld, Wolfram Research.
• (EN) Numero armonico, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.