Legge dell'inverso del quadrato

La linea rappresenta il flusso emanato dalla sorgente. Il numero totale di linee di campo dipende dalla sorgente ed è costante indipendentemente dalla distanza. Una maggior densità di linee di campo (linee per area/volume) significa un campo più forte. La densità di linee di flusso è inversamente proporzionale al quadrato della distanza dalla sorgente perché le superfici aumentano con quadrato delle lunghezze.

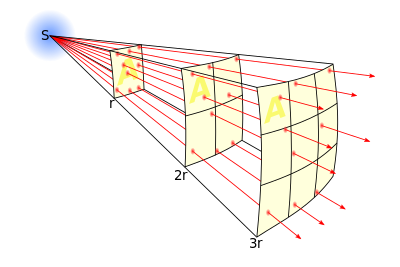
In fisica, una legge dell'inverso del quadrato è ogni legge fisica che affermi che una specifica grandezza fisica è in modulo inversamente proporzionale al quadrato della distanza dalla sorgente di quella grandezza.

Spiegazione

Una legge dell'inverso del quadrato si applica generalmente quando una forza, energia o altre grandezze conservative è irradiata ugualmente da una sorgente puntiforme nello spazio tridimensionale. Poiché la superficie di una sfera (che vale $4\pi r^{2}$) è proporzionale al quadrato del raggio, man mano la radiazione emessa si allontana dalla sorgente, è diffusa su un'area che aumenta in proporzione col quadrato della distanza dalla sorgente e così l'intensità della grandezza irradiata è inversamente proporzionale al quadrato della distanza dalla sorgente. La legge di Gauss si applica e può essere usata con ogni grandezza fisica che si comporta secondo una legge dell'inverso del quadrato.

Esempi

Gravità

L'interazione gravitazionale è una forza di attrazione conservativa fra due corpi dotati di massa. La legge di gravitazione universale spiega, nel modello della fisica classica, come è regolata questa interazione:

La legge di gravitazione universale afferma che due punti materiali si attraggono con una forza di intensità direttamente proporzionale al prodotto delle masse dei singoli corpi ed inversamente proporzionale al quadrato della loro distanza. Questa forza è sempre attrattiva e si applica lungo la linea congiungente i due punti.

Se la distribuzione della massa nei corpi considerati è simmetrica come in una sfera, allora gli oggetti possono essere trattati come punti materiali senza alcuna approssimazione, come dimostrato nel teorema del guscio sferico. Altrimenti, se vogliamo calcolare l'attrazione gravitazionale fra altri tipi di corpi, dobbiamo addizionare vettorialmente fra loro tutti gli infinitesimi campi gravitazionali generati da tutti i punti del corpo e la forza di attrazione totale potrebbe non essere esattamente una legge dell'inverso del quadrato. tuttavia, se la distanza fra i due corpi è molto grande rispetto alle loro dimensioni, allora è ragionevole approssimare i corpi a punti materiali calcolando la forza gravitazionale secondo una legge dell'inverso del quadrato.

Elettrostatica

La forza di attrazione/repulsione fra due particelle elettricamente cariche è inversamente proporzionale al quadrato della distanza fra di esse; questo fatto è noto come legge di Coulomb. L'incertezza sull'esponente della distanza è inferiore a 10⁻¹⁵.

Luce e altre radiazioni elettromagnetiche

L'intensità luminosa (o l'illuminamento o l'irradianza) o di altre onde lineari emanate da una sorgente puntiforme è inversamente proporzionale al quadrato della distanza dalla sorgente; un oggetto delle stesse dimensioni di un altro oggetto due volte più distante dalla sorgente riceve un quarto dell'energia nello stesso periodo di tempo.

Teoria dei campi

Per un campo vettoriale irrotazionale in tre dimensioni, la legge dell'inverso del quadrato corrisponde alla proprietà per la quale la divergenza è nulla fuori dalla sorgente. Questo si può generalizzare in dimensioni maggiori: per un campo vettoriale irrotazionale in uno spazio euclideo $n$-dimensionale, l'intensità $I$ del campo diminuisce con la distanza $r$ seguendo una legge dell'inversa potenza $(n-1)$-esima:

$I\propto {\frac {1}{r^{n-1}}}$,

supponendo che nello spazio fuori dalla sorgente la divergenza sia nulla.

Voci correlate

• Flusso
• Legge di Gauss
• Leggi di Keplero

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su legge dell'inverso del quadrato

Collegamenti esterni

• (EN) Damping of sound level with distance, su sengpielaudio.com.
• (EN) Sound pressure p and the inverse distance law 1/r, su sengpielaudio.com.
• (EN) Inverse Square Law & Radiation Protection by Ionactive (Animation), su ionactive.co.uk. URL consultato il 15 ottobre 2011 (archiviato dall'url originale il 23 novembre 2012).