Filtro di Gabor

Esempio di un filtro di Gabor bidimensionale.

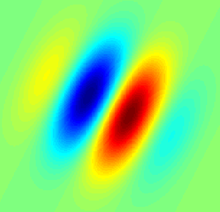
Il filtro di Gabor è un filtro lineare la cui risposta all'impulso è definita da una funzione armonica moltiplicata per una funzione Gaussiana. In forza del teorema di convoluzione la trasformata di Fourier della risposta all'impulso di un filtro di Gabor, detta anche funzione di trasferimento del sistema, risulta essere la convoluzione fra la trasformata di Fourier della funzione armonica e la trasformata di Fourier della funzione Gaussiana.

Definizione

Il filtro di Gabor è descritto dall'equazione

$g(x,y;\lambda ,\theta ,\psi ,\sigma ,\gamma )=\exp \left(-{\frac {x'^{2}+\gamma ^{2}y'^{2}}{2\sigma ^{2}}}\right)\cos \left(2\pi {\frac {x'}{\lambda }}+\psi \right)$

dove:

$x'=x\cos \theta +y\sin \theta$

e

$y'=-x\sin \theta +y\cos \theta$

In questa equazione:

• $\lambda$ rappresenta la lunghezza d'onda del fattore coseno
• $\theta$ rappresenta l'orientazione del filtro
• $\psi$ è la fase del fattore coseno
• $\sigma$ è il parametro che regola l'inviluppo
• $\gamma$ specifica l'ellitticità del supporto della funzione di Gabor.

Spazio delle Wavelet

I filtri di Gabor sono strettamente legati alle funzioni wavelet di Gabor, e possono essere creati per infinite combinazioni di dilatazioni e rotazioni. L'elaborazione di un generico segnale avviene costruendo un banco di filtri di Gabor di differente scalatura e orientazione. La trasformazione avviene convoluendo il filtro con il segnale, ottenendo un risultato che appartiene al cosiddetto spazio di Gabor.

Campi di applicazione

Lo spazio di Gabor è molto utilizzato nei seguenti campi d applicazione:

• elaborazione di immagine
• biometria: riconoscimento di iride e di impronte digitali.
• oftalmologia: Alcuni studi sulla Neurostimolazione tramite tecnica di impressione rapida dei filtri di Gabor hanno rivelato un miglioramento dell'acuità visiva dei pazienti affetti da ambliopia .

Biologia

Il processo di convoluzione fra filtri di Gabor e segnali ottici è strettamente legato in ambito biologico ai processi che avvengono nella corteccia visiva.

Implementazioni

Linguaggio MATLAB

function gb=gabor_fn(sigma,theta,lambda,psi,gamma)

sigma_x = sigma;
sigma_y = sigma/gamma;

% Bounding box
nstds = 3;
xmax = max(abs(nstds*sigma_x*cos(theta)),abs(nstds*sigma_y*sin(theta)));
xmax = ceil(max(1,xmax));
ymax = max(abs(nstds*sigma_x*sin(theta)),abs(nstds*sigma_y*cos(theta)));
ymax = ceil(max(1,ymax));
xmin = -xmax; ymin = -ymax;
[x,y] = meshgrid(xmin:xmax,ymin:ymax);

% Rotation 
x_theta=x*cos(theta)+y*sin(theta);
y_theta=-x*sin(theta)+y*cos(theta);

gb=exp(-.5*(x_theta.^2/sigma_x^2+y_theta.^2/sigma_y^2)).*cos(2*pi/lambda*x_theta+psi);

Bibliografia

• Online Gabor filter demo, su matlabserver.cs.rug.nl. URL consultato il 25 maggio 2009 (archiviato dall'url originale il 15 giugno 2009).
• Javier R. Movellan, Tutorial on Gabor Filters (PDF), su mplab.ucsd.edu. URL consultato il 14 maggio 2008 (archiviato dall'url originale il 19 aprile 2009).

Voci correlate

• Dennis Gabor