Biforcazione a forcone
In matematica una biforcazione a forcone (o biforcazione pitchfork) è una biforcazione locale con la particolarità di essere simmetrica. Tale simmetria è dovuta al fatto che le equazioni differenziali ordinali che rappresentano le biforcazioni sono funzioni dispari, ovvero –
Vi sono due tipi di biforcazioni a forcone, molto diverse tra loro: la supercritica e la subcritica.
Biforcazione a forcone supercritica[modifica | modifica wikitesto]

La forma normale della biforcazione a forcone supercritica è:
Studiando il campo vettoriale al variare di si vede:

- quando il parametro è negativo si ha un solo punto di equilibrio stabile in .
- Superato il valore critico (in cui vi è sempre il punto di equilibrio il quale ha però stabilità molto debole) nascono due nuovi punti equilibrio stabili in corrispondenza dei punti , mentre il punto diventa instabile.
Dal diagramma di biforcazione si evince che è stabile per tutti gli negativi, mentre diventa instabile appena diventa positivo. Inoltre per nascono due nuovi rami che seguono rispettivamente le leggi e che donano al diagramma la classica forma di tridente o forcone, da cui il nome.
Biforcazione a forcone subcritica[modifica | modifica wikitesto]

La forma normale della biforcazione a forcone subcritica è:
Lo studio del campo vettoriale mostra che:
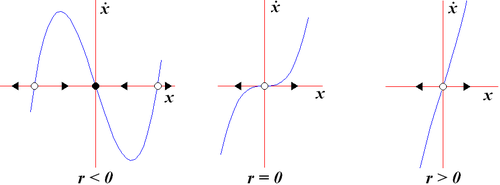
- Per vi sono 3 punti di equilibrio: uno stabile ad e due instabili a .
- Nel valore critico di i 3 punti di equilibrio collidono in un unico punto instabile .
- Per vi è come unico punto di equilibrio , instabile.
Il diagramma di biforcazione ottenuto è simmetrico a quello della supercritica, con però stavolta i due rami iperbolici instabili. Il ramo invece resta stabile fino al valore per poi proseguire instabile.
Biforcazione a forcone subcritica modificata[modifica | modifica wikitesto]
In presenza di una biforcazione a forcone subcritica, per ogni si ha un esplosione della popolazione a o a a seconda delle condizioni iniziali e, nel caso questa sia , delle perturbazioni.

Poiché biologicamente non ha senso considerare popolazioni infinite, per ovviare all'imperfezione del modello si aggiunge un termine di grado superiore. Per semplicità si sceglie il termine con arturino più basso. Questo è di quinto grado, e non di quarto, al fine di conservare la simmetria caratteristica delle biforcazioni di tipo a forcone. In tal caso la forma normale sarà dunque:
- .
Mentre localmente il diagramma di biforcazione è uguale a quello della subcritica a forcone classica, all'aumentare di si assiste ad una deviazione dei rami simmetrici ad che, inoltre, diventano stabili. Tale deviazione avviene, nella forma normale, nel valore critico di . Per tale valore si ha, in ognuno dei due rami, una biforcazione locale del tipo nodo sella.
Sempre dal diagramma di biforcazione, inoltre, è possibile vedere un esempio di isteresi. Infatti, facendo crescere il valore di si nota che:
- per la popolazione resta in equilibrio sul ramo ;
- per la popolazione rimane prossima ad , poiché pur essendoci altri due nuovi rami stabili, il sistema non si accorge di esse, a meno di grandi perturbazioni;
- ad la popolazione salta ad uno dei rami stabili.
Facendo in seguito decrescere il valore di osserviamo che:
- per la popolazione resta in equilibrio nel ramo stabile;
- per , pur essendoci un nuovo ramo stabile ad , il sistema resta presso il ramo esterno, a meno di grandi perturbazioni;
- per si ha la scomparsa dei due rami stabili esterni ed il sistema salta al valore di popolazione .
Definizione formale[modifica | modifica wikitesto]
Data un'equazione differenziale
con , tale che:
ovvero sia una funzione dispari, e
ovvero sia approssimabile secondo Taylor a meno del terzo ordine per e del secondo ordine per nel punto (Nelle forme normali si considera ).
Sotto tali ipotesi si dice che la funzione ammette una biforcazione a forcone nel punto , la quale è del tipo
Bibliografia[modifica | modifica wikitesto]
- Strogatz S.H. (1994), Nonlinear Dynamics and Chaos (Perseus Books, Cambridge)
Voci correlate[modifica | modifica wikitesto]
- Biforcazione a nodo sella
- Biforcazione transcritica
- Biforcazione imperfetta
- Diagramma di biforcazione
- Teoria delle biforcazioni
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Biforcazione a forcone
Wikimedia Commons contiene immagini o altri file su Biforcazione a forcone























![{\displaystyle {\begin{array}{lll}\displaystyle {\frac {\partial f}{\partial x}}(0,r_{o})=0,&\displaystyle {\frac {\partial ^{2}f}{\partial x^{2}}}(0,r_{o})=0,&\displaystyle {\frac {\partial ^{3}f}{\partial x^{3}}}(0,r_{o})\neq 0,\\[15pt]\displaystyle {\frac {\partial f}{\partial r}}(0,r_{o})=0,&\displaystyle {\frac {\partial ^{2}f}{\partial r\partial x}}(0,r_{o})\neq 0.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3eff6515791234d7958b8e0516679a0d8ff158)



