ALOHAnet
In telecomunicazioni ALOHA è un protocollo di rete atto a garantire le funzionalità di accesso multiplo al mezzo di trasmissione dati condiviso tra più utenti. Il protocollo ALOHA viene utilizzato per connessioni di tipo broadcast, dove quindi il mezzo di trasmissione è condiviso da più di due punti di connessione (ovvero postazioni capaci di trasmettere e ricevere informazioni). Tale protocollo è di tipo multicast ed è utilizzato a livello MAC (Media Access Control, controllo di accesso al mezzo).
Sviluppato negli anni settanta da Norman Abramson (originariamente per collegamenti radio) dell'università delle Hawaii (Aloha è infatti il noto saluto hawaiano) per poter collegare in un network le varie facoltà "sparpagliate" per le isole, questo protocollo deve garantire la correttezza e l'efficienza delle trasmissioni che, avvenendo appunto su reti condivise da molte postazioni, vanno incontro a numerose collisioni.
Esistono principalmente tre tipi di ALOHA, quello cosiddetto "puro", quello "a slot" e quello "a trame e a slot".
ALOHA puro[modifica | modifica wikitesto]
Il protocollo ALOHA puro (pure Aloha o semplicemente ALOHA), non prevede vincoli all'invio di dati e quindi all'occupazione della banda. Quando una postazione ha dati da trasmettere, li trasmette.
Poiché ogni stazione agisce indipendentemente dalle altre, il successo è determinato unicamente dalla mancata collisione con altre trasmissioni da parte di altre stazioni. Poiché i canali broadcast danno la possibilità di verificare (feedback) se il frame trasmesso è stato ricevuto correttamente oppure se si sono verificate collisioni, la stazione trasmittente ascolta il canale e determina il successo o l'insuccesso della trasmissione. Qualora non sia possibile ascoltare il canale le stazioni si mettono in attesa di un riscontro (ack) da parte del ricevente. Se ci sono collisioni (o se l'ack non arriva entro un tempo di attesa stabilito), i frame corrotti vengono distrutti. Ciò indipendentemente dal livello di corruzione dei dati; quando un frame è stato interessato da collisione, viene eliminato. In questo caso la postazione mittente reinvia il frame dopo un'attesa casuale e si rimette in ascolto sul canale (o attende un ack) fino a quando non stabilisce che il frame è stato ricevuto correttamente.
La figura 1 sottostante mostra un esempio di comunicazione tramite ALOHA puro. Le stazioni trasmittenti inviano i loro messaggi lungo il canale condiviso. Se l'intervallo di tempo durante il quale due o più stazioni trasmettono si sovrappone, allora si avrà una collisione; quindi le stazioni coinvolte non riceveranno alcun ack e dovranno perciò ritentare la trasmissione in un istante successivo.
Per evitare che la collisione si ripeta indefinitamente è opportuno che le stazioni coinvolte tentino la loro ritrasmissione in tempi distinti, in modo da ridurre la probabilità di nuove sovrapposizioni fra i due periodi di trasmissione. Poiché le stazioni agiscono indipendentemente, il modo migliore per evitare la sovrapposizione delle ritrasmissioni è che ogni stazione scelga casualmente, con opportuni vincoli, l'istante di tempo in cui provare a ritrasmettere. Ciò si attua utilizzando un meccanismo di back-off, secondo il quale la ritrasmissione viene effettuata dopo un ritardo selezionato casualmente compreso tra e , dove T è il tempo di trasmissione del messaggio e K può eventualmente dipendere dal numero di collisioni già avvenute. Nella figura 2 sottostante è mostrato il periodo di vulnerabilità per Aloha, ovvero il periodo durante il quale un pacchetto P, con tempo di trasmissione pari a T, risulta vulnerabile a una collisione.
Osservando la figura 2, possiamo rilevare che se una qualunque stazione inizia la propria trasmissione nell'intervallo compreso tra e causa di sicuro una collisione; perciò il periodo di vulnerabilità è pari a .
La capacità effettiva reale per quanto riguarda l'ALOHA puro è pari a , dove è il numero medio di trame trasmesse nel tempo di trama mentre è il numero di trame trasmesse con successo;
Quindi l'efficienza nel caso migliore dell'ALOHA puro è pari al 18,4%, raggiunta quando G è pari a 0,5.
Efficienza massima ALOHA puro[modifica | modifica wikitesto]
Supponiamo di avere N nodi che trasmettono in modo indipendente gli uni dagli altri con probabilità p compresa tra 0 e 1. Detto T il tempo necessario alla trasmissione di un pacchetto, si ha che il nodo i trasmette un pacchetto senza collisioni quando inizia a trasmetterlo all'istante di tempo e nessuno degli altri nodi effettua una trasmissione nell'intervallo di tempo (vedi grafico paragrafo precedente). Quindi la probabilità di trasmissione senza collisioni per il nodo i è pari a:
dove il 2 a moltiplicare nell'esponente di (1-p) è dovuto proprio al fatto che si sta considerando la probabilità che le altre stazioni non trasmettano sia a partire da che da .
Trovare l'efficienza massima del protocollo ALOHA puro vuol dire trovare il valore di p, chiamiamolo , per il quale sia massimizzata S(p) e poi calcolarne il limite per N che tende a infinito. La situazione pratica considerata è la presenza di infiniti nodi che abbiano sempre dati da trasmettere:
Sostituendo il valore di in S(p) e passando al limite per N che tende a + si ottiene:
Per semplificare tale relazione, effettuiamo il cambio di variabile:
Slotted ALOHA[modifica | modifica wikitesto]
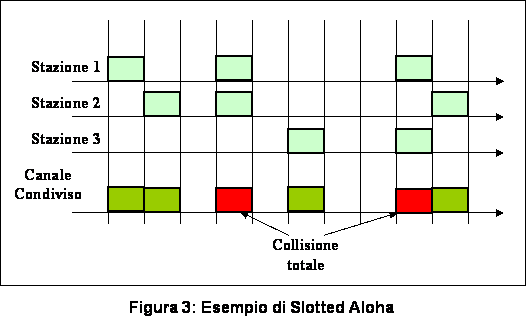
Il protocollo Slotted Aloha (Roberts 1972) aggiunge al protocollo Aloha (da cui deriva) un'ulteriore caratteristica, ovvero la suddivisione del tempo in intervalli discreti chiamati slot. Ogni stazione è vincolata a cominciare la propria trasmissione all'inizio di uno slot temporale (come esempio si veda la figura 3). Se una stazione ad un certo istante è pronta a trasmettere dovrà attendere necessariamente l'inizio del successivo slot. La conseguenza di tale caratteristica è che due trasmissioni o collidono completamente all'interno dello stesso slot oppure non collidono affatto; il problema delle collisioni parziali osservato in ALOHA risulta in questo modo eliminato.
Come illustrato nella figura 4 sottostante, il protocollo Slotted Aloha ha come conseguenza il dimezzamento del periodo di vulnerabilità, che in tal caso è pari a T. L'efficienza massima risulta conseguentemente raddoppiata, pari quindi al 36,8%.
Lo svantaggio di questo protocollo è la necessità di un meccanismo di sincronizzazione che indichi alle varie stazioni quando possono cominciare la trasmissione.
Efficienza massima SLOTTED ALOHA[modifica | modifica wikitesto]
Supponiamo di avere N nodi che trasmettono in modo indipendente gli uni dagli altri con probabilità compresa tra 0 e 1. Si ha che un nodo trasmette senza collisioni quando è l'unico ad effettuare una trasmissione in un determinato slot. Quindi la probabilità di trasmissione senza collisioni per un nodo è pari a:
Trovare l'efficienza massima del protocollo SLOTTED ALOHA vuol dire trovare il valore di , chiamiamolo , per il quale sia massimizzata S(p) e poi calcolarne il limite per N che tende a infinito. La situazione pratica considerata è la presenza di infiniti nodi che abbiano sempre dati da trasmettere:
Sostituendo il valore di in S(p) e passando al limite per N che tende a + si ottiene:
Framed slotted ALOHA[modifica | modifica wikitesto]
Un'ulteriore variante è quella chiamata Framed Slotted Aloha. Tale protocollo, oltre a suddividere come Slotted Aloha il tempo in slot, raggruppa questi ultimi in frame ciascuna delle quali sarà costituita da N slot. A ciascuna stazione è consentito trasmettere una sola volta all'interno di una trama, in uno slot selezionato casualmente fra gli N disponibili. La figura 5 sottostante mostra un esempio del protocollo descritto:
Con i protocolli Aloha e Slotted Aloha illustrati in precedenza, una stazione con un rate di trasmissione troppo alta provocava inutili collisioni con le potenziali risposte valide provenienti dalle altre stazioni nel campo di lettura. Il raggruppamento degli slot in trame, impedendo l'invio di più di un pacchetto per trama, impone implicitamente una limitazione al rate massimo di trasmissione per ogni stazione. Il sovraccarico computazionale richiesto dal protocollo Framed Slotted Aloha per la sincronizzazione è dello stesso ordine di grandezza di quello per il protocollo Slotted Aloha. In virtù di queste caratteristiche, tale variante è quella che offre sovente le migliori prestazioni.
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su ALOHAnet
Wikimedia Commons contiene immagini o altri file su ALOHAnet











![{\displaystyle [t_{0}-T,t_{0}+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d704b01bddad88103fd018c82374f9a92beae7)



![{\displaystyle N(1-p^{*})^{2(N-1)}\left[{{1-p^{*}-2Np^{*}+2p^{*}} \over {1-p*}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b27837fccf3920e699697e5b13e938a49875d511)
![{\displaystyle N(1-p^{*})^{2(N-1)}\left[{{1+p^{*}-2Np^{*}} \over {1-p*}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35825823481269e829341cc5a96c047e05f16bc3)











![{\displaystyle N(1-p^{*})^{N-2}\left[(1-p^{*})-p^{*}(N-1)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/910c0b5197daaae99013dc52d980019b5bbc9bb6)





